三、孙老师与中年教师的我
说起我的工作经历,从1994年至今,一直从事从初一到高三的大循环式的数学教学。现在,我的第三轮学生已经进入高三毕业年级。特别是从2001年至今,我一直担任数学实验班的数学教学和班主任工作。这样的工作经历,使我有机会在实践中不断思考、理解孙老师的教育理念。
很多人问我怎样概括孙老师的教学,我的体会是:孙老师艺术的展现了数学,使数学艺术化。具体说,他最大的特点将数学上升到哲理的高度。表现在两个方面:一个是整体把握中学数学,另一个是运用普遍联系的观点使数学成为一个有机的整体。
关于孙老师的课堂教学的风格,经过十几年的探索和思考,我概括为:深入本质和和谐交流。基于对孙老师的不断理解,我也逐步地调整自己,使自己尽可能地向孙老师学习,尽可能地像他那样教书育人。下面我举我的两个教学案例,想表达我对孙老师的理解使我在具体工作中,做出了我认为的较好的教学策略的选择,就算是对老师的汇报吧。
案例1:某次考试有一道题:
已知函数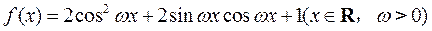 的最小正周期是
的最小正周期是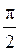 .求函数f(x)的单调递增区间;
.求函数f(x)的单调递增区间;
某学生求出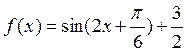 后,求函数f(x)的单调递增区间出现了下面的错误:
后,求函数f(x)的单调递增区间出现了下面的错误:

面对这种错误,课堂上我引导学生分析:为什么会出现这种错误呢?学生分析可能性一:与求值域问题混了;可能性二:与图像变换问题混了。我首先引导学生讨论:
师:求值域问题的方法是什么?
生:求函数值域可以通过函数图像观察,也可以由函数定义域和函数解析式,通过运算计算出函数值域。例如:已知x∈[a,b], ,进而算出
,进而算出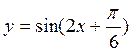 的值域。
的值域。
师:为什么求值域问题用这样的方法?
生:是由函数概念决定的。定义域和对应法则是决定函数值域的两个要素。
师:该生为什么与图像变换问题混了?混在哪个环节了?
生:图像变换也是要考虑y=sin x,y=sin 2x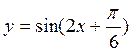 三个函数之间的关系,但此方法是将y=sin x的x视为y=sin 2x中的2x,由y=sin x的单调区间得到y=sin 2x的单调区间,再将y=sin 2x中的x视为
三个函数之间的关系,但此方法是将y=sin x的x视为y=sin 2x中的2x,由y=sin x的单调区间得到y=sin 2x的单调区间,再将y=sin 2x中的x视为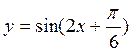 中的
中的 进而得到
进而得到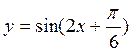 得单调区间。这一过程与通过运算求函数值域表面看有相似之处,但本质是截然不同的。
得单调区间。这一过程与通过运算求函数值域表面看有相似之处,但本质是截然不同的。
接着,我再进一步引导学生思考为什么下面的两种方法都是正确的?
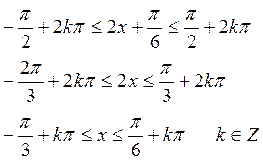 方法1 :
方法1 :
方法2:
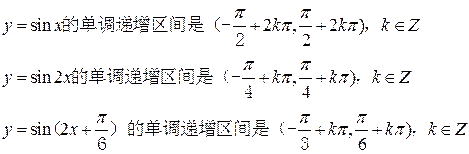
学生分析得出两种不同的方法都是将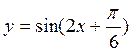 视为
视为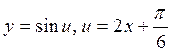 本质都是应用复合函数单调性的概念。
本质都是应用复合函数单调性的概念。
案例评述:孙老师说:“题不在多,但求精彩”。所谓的精彩,我觉得有一个方面是怎样使学生在错误中汲取营养。有的老师对孙老师不留硬性的家庭作业,不做反反复复的练习,学生成绩却那样的好,觉得神奇。其实没有那么玄妙,只不过是一些重要的细节我们太多的人忽视了,而孙老师意识到了、扑捉到了、真正做到了。我在实践中渐渐理解教学中教师应有意识的引导学生学会正确的分析诊断自己的错误。我们发现往往是那些能力强、成绩好的学生错误反复出现的情况很少,而那些能力欠佳、成绩令人担忧的学生错误的反复率很高,这与他们对错误的恰当分析、诊断、认识的能力是相关的, 教师可以利用一些典型错误进行分析,提高学生对相关知识及知识之间的联系的认识。
案例2:
背景:某学生课下来问我一道题如何做,题目是这样的:已知A(2,-5,3), B(1,t5-t), c(t-1,3,t+2) 三点共线,求t的取值。
以下是我们师生对话的内容:
生:此题不会做。
师:你想到了哪些?
生:平面内证明三点共线的方法
师:很好啊!你能把立体问题转化为平面问题,具体说说
生:我可以用两点写直线方程,然后将第三个点的坐标代入,满足方程证明三点共线
师:哦,我明白了,你打算把它类比到空间来证明三点共线。这种类比的意识很好,可为什么不行呢?
生:(沉思片刻有些犹豫)我不会写空间的直线方程
师:为什么呢?是什么原因?是你忘了还是什么?
生:我们没有学过
师:我们都学过什么相关的知识?换句话说,我们研究的范围是什么?
生:平面直角坐标系下学过很多,研究过很多问题,空间直角坐标系学过一些知识
师:空间直角坐标系学过什么?
生:点的坐标表示、空间向量、立体几何的证明和计算
师:说得好啊!空间直角坐标系下直线的方程学过吗?
生:没有
师:这是我们现有知识的局限性,明白为什么你目前做不出此题了吗?
生:明白了
师:那你打算怎么办?
生:用向量作
师:具体说说
生:类比平面向量,写出向量AB、向量BC,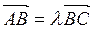 ,解出此题
,解出此题
师:会做了,很高兴吧
生:微微一笑,点头同意,
师:这题难吗?
生:不难
案例评述:
以上交流可以将教师的作用概括为以下三点:
1、 及时地给予恰当的肯定,增强学生探索、深入思考的信心。心态很重要,灵感的火花很难在压抑的状态下迸发
2、 引导学生“退”——对知识、经验、方法的回顾。将具体问题所涉及的知识还原到整体知识框架中,引导学生站在系统的高度从整体的观点分析思考知识之间的联系,随着情节的推进,在资源与目标之间建立起有效的桥梁,即形成了解决问题的思路方法
3、 引导学生不断地从特殊到一般、具体到抽象、感性到理性变换角度思考
教学过程中,经常会有学生带着问题向老师请教,我们不要忙于给学生讲此题应该怎样做,而应向孙老师那样给予学生最需要的、最关键的内容,孙老师的睿智表现在他对学生的心里非常了解,他总能在最恰当的时候以最恰当的方式给予学生最恰当的帮助。面对困境中的学生我们把重点放在引导学生在自己原有认知基础上想方设法走出困境,给学生享受走出困境的快乐、喜悦的机会,使学生相信我也具有了解决此问题的能力。即使学生认为自己的想法一无是处,教师也要竭尽全力的帮助他发现自己思维价值的闪光点。教师还应注意到:当学生来问我们问题时,学生的注意力往往在具体的解题方法上,而忽视了方法是怎样产生的,这一点教师应及时地提醒学生。
四、孙老师与未来的我
孙老师离开我们十年了,十年来对他的不断追忆,使我渐渐明白了一件事:恩师对我最大的影响,还不是数学,而是价值观。它不仅影响了我的过去和现在,未来的日子,恩师的教诲依然是我行为的准则,他给我信心和力量。
五、我所理解的孙维刚教育思想与当代教育理念
作为一名教育工作者,我在实践孙老师的教学模式的同时,也从来没有放弃过参加各类培训和学习的机会,在不断的与专家、学者的交流讨论的过程中,我深深感觉到很多现在我们提倡的教育观念,与几十年前孙老师所倡导的思想、观点竟然不谋而合,孙老师他超越于那个时代的关于教育、社会、人生的思考,真的需要我们认真研究。
未来的路需要我们不断的思考、实践。愿我们所作的一切孙老师能够感知到!